Stanford EE364A Convex Optimization I Stephen Boyd I 2023 I Lecture 3

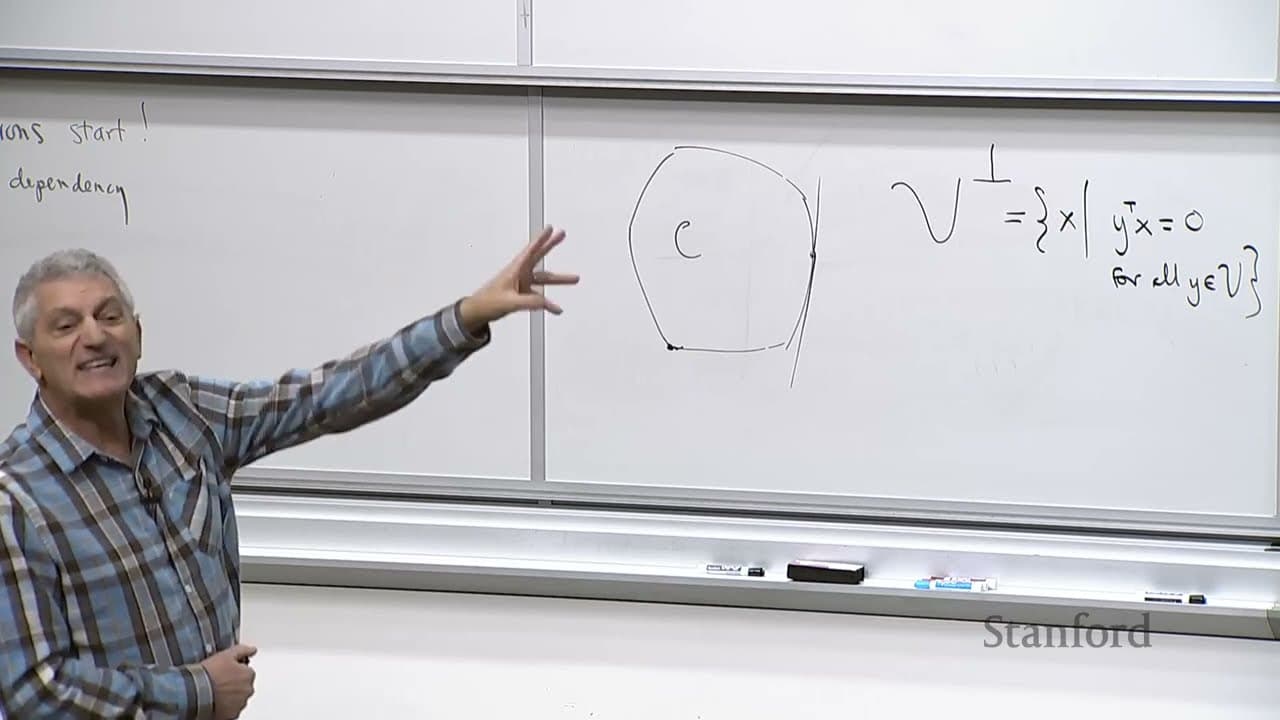
Convexity and Optimization

• Homework 1 is challenging, but students should not spend excessive time on any one problem.
• The course will become more interesting after this week's slog through math.
• The course will approach convex optimization from a calculus perspective, which is both mathematically sound and actionable in code.

Vector Inequalities

• Vector inequalities are not linearly or totally ordered like real numbers.
• The minimum of a set of vectors is a point where everything else in the set is comparable and larger than or equal to it.
• A minimal element is a point where there is no other point in the set that is less than or equal to it, except itself.

Hyperplanes

• A separating hyperplane divides two sets in a vector space such that one set lies entirely in one half-space and the other set lies entirely in the other half-space.
• Every convex set has a supporting hyperplane at every point of its boundary.
• The converse of the above statement is also true: if a set has a supporting hyperplane at every point of its boundary, then it is convex.

Duality

• The dual cone of a cone K is the set of all vectors that have a non-negative inner product with every vector in K.
• The dual of the dual of a subspace is the original subspace.
• A self-dual cone is a cone that is equal to its own dual cone.

Minimal Points and Production Sets

• A minimal point of a set is a point that minimizes a linear function over the set for any positive weights in the dual cone.
• A production set is a set of all feasible choices for producing a product.
• A point in a production set is efficient if there is no other point in the set that uses less of each resource to produce the same amount of output.

Convex Functions

• A convex function is a function from Rn to R whose domain is convex and satisfies the inequality f(tx + (1-t)y) ≤ tf(x) + (1-t)f(y) for all x, y in the domain and t in [0, 1].
• Convexity means non-negative curvature of a function.
• A function is concave if its negative is convex.
• A function is strictly convex if the inequality F(θx + (1-θ)y) < θF(x) + (1-θ)F(y) holds strictly for all 0 < θ < 1.
• Convexity implies that the function value at a mixture of points is less than or equal to the mixture of function values.
• Norms in RN are convex functions.
• The spectral norm, or two-norm induced norm, of a matrix is a convex function.
• Convex functions can be gracefully extended to handle the infinity in the domain by defining a new function that returns infinity outside the domain. This allows for the use of infinity values to express constraints.
• The exponential function is the simplest convex function that most people are unaware of.
• The function X^2/Y is jointly convex in x and Y.
• A function of two variables is convex if it is convex in each variable when the other is fixed.
• The converse of the above statement is false. A function can be convex in each variable when the other is fixed but not jointly convex.
• The log-sum-exp function is convex and has applications in various fields.
• The geometric mean of many variables is a concave function.

Convexity and Calculus

• Traditional conditions for convexity are based on calculus and involve the gradient and Hessian matrix of the function.
• The gradient of a function is the set of all partial derivatives.
• The first-order Taylor expansion of a convex function is a global lower bound.
• For a twice-differentiable function, the Hessian is a symmetric matrix of all partial derivatives.
• A function is convex if and only if its Hessian is positive semi-definite at all points.
• The Hessian is a measure of the curvature of a function.
• Determining if a function is convex can be done by checking the second derivative, but this should only be done as a last resort.

Convexity Analysis

• Convexity analysis is a constructive approach to proving the convexity or concavity of functions without using gradients or the basic definition.
• There are a limited number of "atoms" or basic convex functions that can be combined using calculus rules to construct more complex convex functions.
• Some of the calculus rules for combining convex functions are simple and intuitive, while others are more complex and interesting.
• All the calculus rules for combining convex functions can be derived from a single main rule, which is also the basis for constructing code to verify the convexity or concavity of functions.
• Examples of basic convex functions include log, X, log sum X, and log determinant.