Stanford EE274: Data Compression I 2023 I Lecture 5 - Asymptotic Equipartition Property

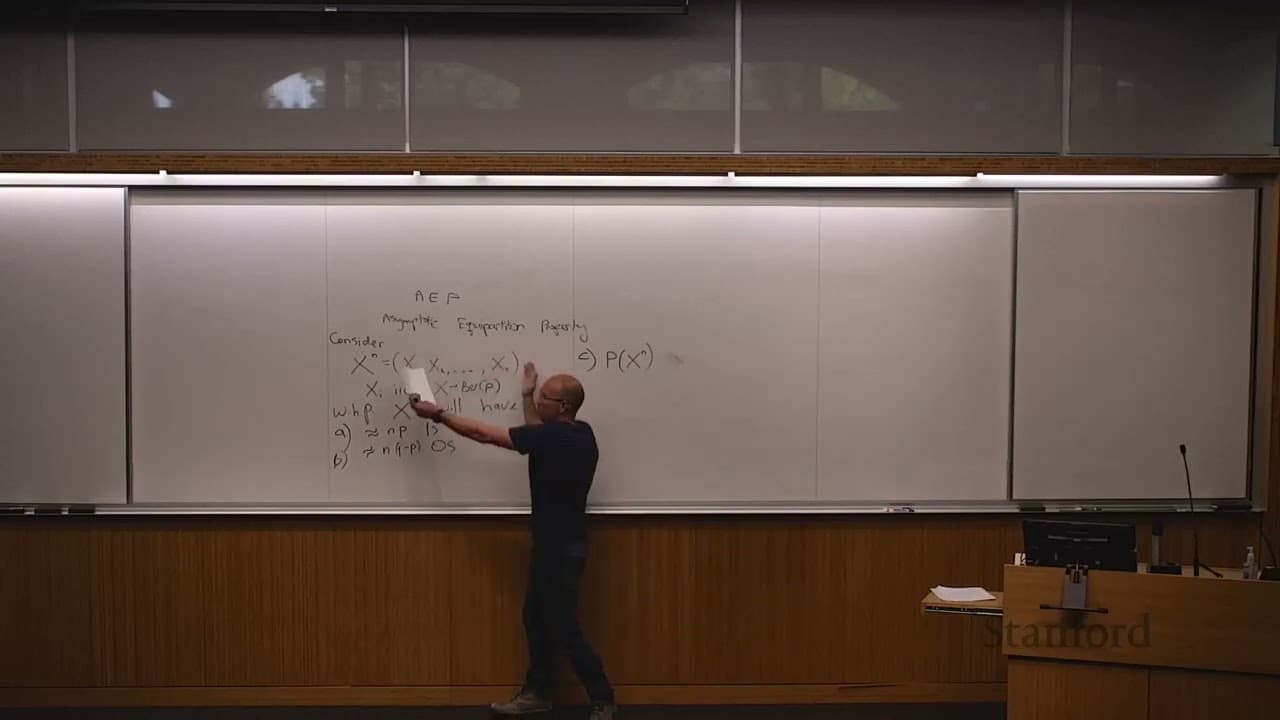
Asymptotic Equipartition Property (AEP) and Compression

• The speaker introduces the concept of the asymptotic equipartition property (AEP) and its relation to compression loss and fundamental limits on compression.
• The AEP states that for large n, the typical sequences have a uniform distribution with probability approximately 2^(-nH), where H is the entropy of the source.
• It is impossible to achieve lossless compression with fewer than H bits per source symbol.
• A compressor cannot achieve lossless compression if the rate (R) is less than the entropy (H) of the source.
• The probability of a source sequence falling within the set of sequences that a compressor can reconstruct is negligible if R is less than H.

Typical Sequences and Entropy

• The speaker provides an example of an IID sequence of binary data generated according to a Bernoulli parameter P.
• The speaker explains that with high probability, the sequence will have approximately nP ones and n(1-P) zeros.
• The speaker defines typical sequences as those sequences whose probability is approximately 2^n times the entropy of the source.
• The typical sequences are a small subset of all possible sequences, with a size of approximately 2^nH, where n is the length of the sequence and H is the entropy of the source.
• The entropy of a biased source is less than one, and the fraction of typical sequences that can be seen with non-negligible probability is exponentially small for large n.

Huffman Coding

• Huffman codes are used in various common algorithms, including JPEG, for entropy coding.
• Fixed Huffman codes are predefined and embedded in formats like gzip, avoiding the need to transmit probability distributions.
• Canonical Huffman codes are sorted by codeword length and lexicographically for the same length.
• Canonical Huffman codes only require the lengths of the codewords to reconstruct the codebook, eliminating the need to transmit probabilities or the tree structure.
• Huffman codes are not necessarily optimal for every sequence realization, but they provide the minimum expected length for a given source.
• The optimality of Huffman codes is defined in terms of expected length, not for every particular sequence.

Comparison with Block Codes

• Block codes can achieve better compression than Huffman codes for specific sequences, but Huffman codes are optimal in expectation.